Cosmological Forecast and
Its Practical Significance

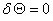
over all possible civilization's histories describes the desired future in the most general form.[2] However, it is illusory to hope to explicate the functional Q in such general terms. Instead, we shall use a greatly simplified “temporal” model, in which we assume that the civilization is characterized by discrete individual observers, countable (with their observer-moments) at any given time. This may be mathematically expressed as:

                                       (*)

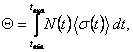where N(t) is the number of observers at epoch t of cosmic time, and áσ(t)ñ the corresponding average density of their observer-moments.[3] The lifetime of the civilization considered spans the interval from t_min to t_max, where the upper limit may—in principle—be infinite. It is important to emphasize that we use physical time here (i.e. we acknowledge validity of Weyl postulate which enables one to define universal, “cosmic” timescale), although it is possible to change coordinates to some subjective timescale if more appropriate, in the manner of Dyson's biological scaling hypothesis (Dyson 1979; Krauss and Starkman 2000), or Tipler's Omega-point theory (Tipler 1994).[4] There are at least two distinct ways in which cosmological parameters enter into eq. (*):

            1. Most obviously, values of cosmological parameters determine absolute limits on t_min and t_max. If the entire lifetime of the universe is equal to t, than t_max £ t. In addition, t_min > 0, but also one may state that t_min ³ t_*, where t_* is the epoch of formation of first stars of sufficiently high metallicity for processes of chemical and biological evolution to take place.

            2. The shape of the function N(t) is dependent on the cosmological parameters when the nature of matter distribution is taken into account. Namely, the power spectrum of density perturbations determines which objects form as result of gravitational attraction and decoupling from the universal Hubble expansion (for a modern textbook treatment see Peebles 1993). On the other hand, the size of the matter aggregates like stars, galaxies, etc. is essential for answering the question how large parts of the rest mass can be converted into energy for purposes of (intelligent) information processing. It is plausible to assume that the maximal number of observers is proportional to the energy consumed for such purposes, which can be mathematically written as

                                 (**)

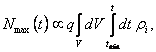where r_i denotes the relevant energy density, and q < 1 is the efficiency of whatever energy extraction process used by the civilization. The reason why we consider the maximal number of observers is that the exact number, of course, depends on the sociological factors which are completely outside of the scope of the present study. It may also strongly depend on the level of technology (e.g. Sandberg 2000), and may radically decrease with the further scientific and technological advancement (like in the cyberpunk scenarios of “collective consciousness” development). Neglecting this, we perceive that at least this upper limit is still cosmologically determined, since both relevant densities r_i and integration bounds are contained in the cosmological discourse. Of course, the density áσ(t)ñ is even less tractable from the point of view of the present knowledge, since it may be expected to hinge crucially upon biological factors on which we know little. However, for the purposes of present study, it is enough to assume that it is non-zero function of time which either increases or decreases slower than exponential.

3. COSMOLOGICAL REVOLUTION: A STORY

How does the number of observer moments Q tally with various cosmological models, including the realistic one? Let us first note that it may be doubted whether such thing as the exact model can ever be reached. Several simplifications come handy at this point. Sufficiently high degree of symmetry leads to familiar Friedmann models (or generalization of them including the cosmological constant), and sufficiently small perturbations can be treated in a familiar way. However, even the general outline on which the future fate of a universe depends may not be obvious till some critical epoch to any internal observers. In particular, as discussed in detail in an illuminating essay by Krauss and Turner (1999), realistic universes are notoriously difficult to analyze completely, due to possible presence of very large (super-horizon) perturbations which enter the visible universe only at some later epoch. From the point of view of internal observers, there is no possibility to avoid this ambiguity. In such position, it is natural that priorities leading to maximization of the number of observer-moments in (*) are contingent on the contemporary cosmological knowledge. As Krauss and Starkman (2000) vividly put it, “funding priorities for cosmological observations will become exponentially more important as time goes on.”

            Let us investigate the following imaginary situation. A civilization inhabiting a particular, sufficiently symmetric universe, develops both theoretical and observational astronomy to the point where it can make useful working models of their universe as a whole. After an equivalent of Einstein of that particular world develops formalism describing curved spacetime at the largest scales, an equivalent of Hubble discovers universal expansion, and equivalents of Penzias and Wilson discover the remnants of primordial fireball, leading cosmologists begin to support the flat baryonic universe with Ω_B = Ω » 1. At first it seems that all observations can be accomodated in the framework of such a model (we suppose that light elements' abundances, for instant, are not inconsistent with such high baryonic density, contrary to the situation in our observable universe!). Some circumstantial support for this model comes from ingenious theoreticians of that civilization, who discover that coupling of a universal scalar field to gravity leads to the exponential expansion during the very early epochs. This inflationary phase in the history of such a universe leads to prediction that ïΩ - 1ï = e » 10^-5, while it is not clear whether the universe is marginally closed or marginally open. In the latter case (favored by most of the theoreticians in such a universe), the number of galaxies in their universe is infinite, and therefore such a universe offers a very optimistic prospects for survival of intelligence and life. There is no event horizon in such universe, and the particle horizon is (very) roughly given as the age of the universe in light years, i.e. the maximal path traversed by light along the observer's past light cone. What are prospects of intelligent beings to survive indefinitely in such a universe?

Gradually, bolder scientists begin to tackle physical eschatological issues. An equivalent of Dyson in that world reckons that this civilization can, in principle, indefinitely survive while exploiting sources of energy in larger and larger volume (t_max = ¥). In addition, it was suggested by some extremely speculative and ingenious cosmologists, that non-zero cosmological shear can be manifested at later epochs, providing in this manner additional energy which will be proportional to the volume of the technologized space (although this option has not been studied enough). Predominant attitude toward maximization of (*) is, therefore, very optimistic and not characterized by any sense of urgency. There are physical grounds to expect Q_max = ¥.

            Suddenly, a new and unexpected twist occurs. New cosmological observations, and in particular two superbly designed projects detecting standard candles at large distances in order to make the best-fit estimate of the Hubble constant, indicate a spectacular overthrow of the ruling paradigm. After the dust settles (which lasts for years, and probably decades), the new paradigm suggest that the universe is still geometrically flat, but dominated by the cosmological constant term Λ in such way that W = W_B + W_L = 1, W_B = 0.1, W_L = 0.9. Now, the situation radically changes with respect to the envisaged number of possible observer-moments given by (*). The universe is now found to possess not only a particle, but an event horizon also, defined as the surface through which any form of communication is impossible at all epochs. This is a consequence of the fact that after a phase of power-law expansion, the exponential expansion generated by L sets in, thus creating a second (future and final) inflationary phase in the history of the universe (see Appendix I for some technical details).

            There are further bad news for such a civilization. The decrease in the metabolic temperature envisaged by the Dyson-equivalent can not continue indefinitely, as was possible before the “cosmological revolution”, since the de Sitter universe possesses a minimal temperature, a circumstance following from the quantum field theory, and described in some detail in the Appendix I. This is an extremely small temperature, but still finite, and below it nothing can be cooled without expending precious free energy. Thus, the temperature scaling may be continued only to the final value of t_max in (*). In addition, one may not use any shear energy, since the equivalent of the so-called “cosmological no-hair” theorem guarantees that no significant shear remains during the exponential expansion (Gibbons and Hawking 1977).

            It seems obvious that the “cosmological revolution” will have important social and political consequences if the desire of maximizing Q in (*) remains the legitimate goal of considered civilization. There could be no more leisurely activities in the framework of the second paradigm. Although the survival cannot be indefinite, it still seems that it can be prolonged for very, very long time—but only if one starts early enough. Besides funding for cosmological observations, one may expect that funding for interstellar and even intergalactic expansion will suddenly rise. Colonization of other stellar and (ultimately) galactic systems should better start early in the Λ-dominated universe! 

4. DIFFICULTIES INVOLVED IN ESTIMATES

This story can teach us several lessons. It seems that we are currently in the middle of the “cosmological revolution” described above, although not as dramatic, since there was never a consensus on the values of cosmological parameters or the nature of matter constituents in the actual human cosmology. Also, the currently inferred value for the vacuum density W_L is somewhat smaller, being about 0.7 (e.g. Perlmutter et al. 1999; Zehavi and Dekel 1999). However, the qualitative nature of the revolution and the implied potential change in the entire spectrum of human social and technological activities are analogous.       

Of course, this counterfactual example may be regarded as rather conservative. One may imagine much more drastic changes in the dominant cosmological paradigm. Let us, for instance, suppose that for some reason most cosmologists did accept classical steady state theory of Bondi, Gold and Hoyle in late 1940’s, and that in the same time the development of radio astronomy has been damped for several more decades. The attitude of humanitarian thinkers seeking to maximize Q could be very well encouraged by the steady state concept of creation of low-entropy matter in the manner conserving density of matter fields. Not only did one have t_max = ¥, one should also expect lim_t®¥ N(t) = ¥, and there would have been no plausible reason to expect s(t) to be anything but constant or even increasing function of time. From the particular human point of view, therefore, the steady state cosmology offered one of the most optimistic visions of the future.[5] (This is somewhat ironic, since the steady state model predicts essentially the same exponentially expanding spacetime as the Λ-dominated models.) As we know, after the fierce cosmological battle in 1950’s and early 1960’s, the steady state theory has been finally overthrown by discoveries of QSOs and the cosmic microwave background, as described in a colorful recent history of Kragh (1996). There has been no historical consensus about the exact cosmological model accounting for observations ever since, but it seems that we are on the verge of reaching one. However, it is conceivable that cosmology of some other civilization passes directly from the steady state into the Λ-dominated paradigm. This seems, curiously enough, at least in one respect easier and more natural than what has occurred in actual history (see Appendix II). This paradigm shift must be accompanied by a shift in technological and social priorities if one expects Θ to be maximized.

However, changes in cosmological paradigm currently underway in the real world should not be regarded as the end of the story. As mentioned above, perturbations of the scale larger than horizon scale are expected to enter our visible universe only at some late epochs. In the light of the argument above, one may expect that whatever the cosmological paradigm is established on the timescale of next ~10¹ years, may be upset by observing the perturbations on superhorizon scales (Krauss and Turner 1999). A recent intriguing study of Tipler (1999) shows that cosmological conclusions reached by local observations (i.e. those in the vicinity of the Milky Way) can be highly misleading, and that one should be on guard with respect to results of any local measurement of cosmological parameters.

            Let us try to estimate the effects of belated technologization to the lowest order. It perhaps goes without saying that any such estimate is notoriously difficult, speculative and on the very fringe of the domain of founded scientific speculation; some of the reasons, already mentioned, include our almost perfect ignorance of the evolutionary possibilities in the social domain, as well as the influence of various technological advances on the average census of observer-moments per observer, áσ(t)ñ. Even the simpler part of the problem, the estimate on the possibilities and modes of evolution of the number of observers N(t), poses almost intractable difficulties. We may be virtually certain that the current exponential population growth of humanity will be arrested at some future date, but whether it will result in transition to some other (power-law?) growing function, or tend to a stable asymptotic limit is impossible to establish at this time. There are certainly several timescales relevant for the history of an advanced technological community, which are related to the “quantized” nature of physical resources alluded to above (and which are, ultimately, consequences of the cosmological power spectrum). This may roughly correspond to Kardashev's famous classification of advanced intelligent communities into three types, depending on the energy resources available (e.g. tarter 2001 and references therein). However, there has been no estimates of the timescales required for transition between the types (and possible intermediate timescales corresponding to radically new technologies of energy extraction).

Baryonic mass of the Local Supercluster (henceforth LS) is of the order of 10¹⁵ solar masses (Oort 1983, and references therein), and its luminosity several times 10¹² solar luminosities. Let us suppose that humanity will eventually technologize the entire spatial volume of LS, and gather all its negentropy resources for information processing. Let us also suppose that at whatever time humans (or posthumans) embark on the process of galactic and intergalactic colonization, the historical path of such colonization will be essentially the same; this is a reasonable assumption, since we expect that colonization timescale is significantly smaller from the cosmological timescales characterizing large-scale changes in the distribution of matter within LS. If we further assume (as many of the prominent anthropic thinkers, following Carter’s well-known argument, do) that we are the first technological civilization within LS, we may ask the question how many observer-moments (or conceivable human lives and experiences) we loose by postponing the onset of colonization by Dt? The simplest (“zero-order”) estimate is just to assume that all entropy produced by physical processes in LS during that interval is proportional to the loss of information from the “pool” available to the presumed “Type IV” future hypercivilization (i.e. the one exploiting the energy resources of LS). Major entropy producing process at present (and on the timescales relevant to the issue; see Adams and Laughlin 1997) is stellar nucleosynthesis. Its products are high-entropy photons escaping to intergalactic (and intersupercluster) space and being there further redshifted due to the universal expansion. Using the Brillouin (1962) inequality (essentially the integral version of eq. (**)), we may write

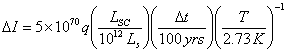bits,

where 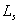is the Solar luminosity, and q is the (time-averaged) fraction of free energy which the hypercivilization converts into work of its computing devices. We expect that the temperature T at which computations are performed to be close to the temperature of the cosmic microwave background since the timescale even for colonization of a huge object like LS is short by cosmological standards, and thus such colonization is essentially isothermal. The quantity of information lost per a century of delay in starting the colonization is astonishing by any standard. For a conservative estimate of q = 0.1, and using Dyson’s (1979) estimate of “complexity” of an average present-day human being 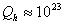bits (quantity which is likely to grow in future, especially in the posthuman stage, but which is still useful as a benchmark), the number of potentially viable human lifetimes lost per a century of postponing of the onset of galactic colonization is simply (if we assume that the luminosity fraction in the equation above is unity, which is probably an underestimate for a factor of a few)

            . (!!!)

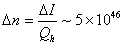Of course, this is only the total integrated loss; if for some currently unknown reason the colonization of LS is impossible or unfeasible, while colonization of some of its substructures is possible and feasible, this huge number should be multiplied by fraction of accessible baryonic matter currently undergoing significant entropy increase (essentially luminous stars). On the other hand, our estimate is actually conservative for the following reasons. There are other entropy-producing processes apart from stellar radiation (notably the stellar black-hole formation becomes more and more important as the time passes), and thus our estimate is actually very conservative, since the lost quantity of information is likely to be higher. Another reason why this estimate should be taken as the absolute lower limit is the entire spectrum of existential risks (see Bostrom 2001b), which have not been taken into account here. Namely, the realistic history of posthuman civilization would be the convolution of the integrand functions in (*) with a risk function f_risk(t) describing the cumulative probability of existential risks up to the epoch t (and their presumed impact on the observer-moment tally). Obviously, this function would be biased toward higher values at small values of t (as measured, for instance, from the present epoch for humans), since smaller—i.e. those not colonizing the universe—civilizations are more prone to all sorts of existential risks. Thus, the risk inherent in “colonization later” policy makes our estimate very conservative (or “optimistic” from the point of view of lost observer-moments). However, this estimate possesses the virtue of being a natural extension of the Dyson’s concept of development of a Type II (Kardashev) civilization: in order to truly technologize domicile planetary system, an advanced society must strive to capture and exploit the entire stellar energy output of its home star, via Dyson spheres or similar contraptions (Dyson 1960). Mutatis mutandis, the same arguments apply to larger scales of density fluctuations, and in the L-dominated cosmological model we are supplied by a natural cut-off at large scales.

5. SUMMARY

The above testifies to the simple truth that awareness of the cosmological situation is a first step toward true long planning for any community of intelligent observers interested in self-preservation and achieving maximum of its creative potential. However, in an evolving universe, the factor of timing seems to set stringent limits on the efficiency with which such intelligent communities are fulfilling their goals. While those limits are certainly to be subject of much debate and discussion in the future, the very fact of their existence makes cosmology interesting from a transhumanist perspective. Decision-making performed today, as far as humanity is concerned, may have enormous consequences on very long timescales. In particular, an overly conservative approach to space colonization and technologization, may result (and in fact might have already resulted) in the loss of substantial fraction of all possible observer-moments humanity could have had achieved. It is our modest hope that this cursory study will contribute to the wider and livelier discussion of these issues and reaching other, more precise predictions for intelligence’s cosmological future.

Finally, let us note that this approach is not necessarily the only manner in which cosmology may enter our everyday life. If some approaches in the fundaments of quantum mechanics and its links to the human conscience are correct, we may find ourselves in a situation where the cosmological boundary conditions determine the nature of our perceptions and self-awareness (Wheeler 1988; Dugić, Raković and Ćirković 2000). This differs markedly from our approach in this essay, which is based on classical cosmology (as well as classical logic and probability theory). One may imagine that the future correct physical theory of conscience will incorporate these elements, and that they will a fortiori play some role in any policy-making attempts based on such a theory.

APPENDIX I

Behavior of universe with large positive vacuum energy density—commonly (and somewhat imprecisely) known as the cosmological constant—L has been investigated in several publications even before the cosmological supernovae began to throw light on its reality (Carroll, Press and Turner 1992; Krauss and Turner 1999; Ćirković and Bostrom 2000). In the L-dominated epoch, the scale factor behaves according to the de Sitter law, i.e.

            ,

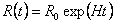where the effective Hubble constant is given as 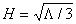. In such a universe, after a transition period between matter-domination and vacuum-domination, the event horizons of the size given as: 

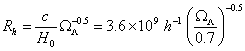pc,     

where c is the speed of light, H₀ º 100 h km s^-1 Mpc is the present-day Hubble constant (parametrized in such way that h is dimensionless number of order unity), and W_L is the cosmological density of vacuum. Beyond this distance no communication is possible at any time. This is very different from the situation in the matter-dominated universes, where the contribution of cosmological constant is very small or completely vanishing, where there are only so-called particle horizons, representing temporary obstacles to communication (i.e. any two arbitrarily chosen points will get into region of causal influence in finite time).

Minimal temperature of the exponentially expanding (de Sitter) universe characterized by cosmological constant L is given by the equation (Gibbons and Hawking 1977):

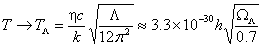 K,                                     (I. 2)

where k is the Boltzmann constant. The expression under the square root on the right-hand side of (I. 2) is close to unity, and h » 0.6. Therefore, this temperature is low beyond description, but as longer and longer timescales in the future unfold, its finite value precludes the asymptotic process of lowering metabolic rate of intelligent creatures of far future suggested by Dyson (1979) as a method for achieving immortality (Krauss and Starkman 2000).

APPENDIX II

Ironically enough, it would not be so extremely difficult to confuse the classical steady-state cosmology with L-dominated ones if the level of sophistication of (neo) classical cosmological tests (e.g. Sandage 1988) is not very high. Namely, the major observational parameter used in empirical discrimination between world models is the decceleration parameter q₀, defined as

            ,

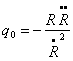where R is the cosmological scaling factor. Of course, this definition is not of much practical value. Instead, it can be shown that in standard relativistic Friedmann-Robertson-Walker cosmologies, q₀ is related to densities in matter and vacuum in the following way (with the usual assumption of negligible pressure):

,

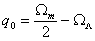which delivers the “classical”  value of 0.5 for Einstein-de Sitter model (W = W_m = 1, W_L = 0), but becomes strongly negative for the vacuum-dominated models. In particular, for the extreme model considered above (W_m = 0.1, W_L = 0.9), we have

            q₀ = – 0.85.

It is well-known that, on the other hand, the decceleration parameter in the steady-state model is

q₀ = const. = – 1.

Obviously, the last two values are close enough for the clear and unequivocal discrimination between them to be an extremely hard observational task.

Acknowledgements. I use this opportunity to express my gratitude to Olga Latinović, Vesna Milošević-Zdjelar, Srdjan Samurović, Milan Bogosavljević and Branislav Nikolić for their help in finding some of the references. The manuscript enormously benefited from discussions with Nick Bostrom, Petar Grujić and Fred C. Adams. Kind advice of Robert J. Bradbury, Mark A. Walker and Mašan Bogdanovski is also appreciated. Technical help of my mother, Danica Ćirković, has been invaluable in concluding this project.

References

Adams, F. C. and Laughlin, G. 1997, Reviews of Modern Physics 69, 337.

Adams, F. C. & Laughlin, G. The Five Ages of the Universe (The Free Press, New York, 1999).

Barrow, J. D. and Tipler, F. J. 1986, The Anthropic Cosmological Principle (Oxford University Press, New York).

Bondi, H. and Gold, T. 1948, Monthly Notices of the Royal astronomical Society 108, 252.

Bostrom, N. 2001a, Synthese 127, 359.

Bostrom, N. 2001b, preprint available at http://www.nickbostrom.com/existential/risks.pdf.

Bostrom, N. 2002, Anthropic Bias: Observation Selection Effects (Routledge, New York).

Brillouin, L. 1962, Science and Information Theory (Academic Press, New York).

Ćirković, M. M. 2000, Serbian Astronomical Journal 161, 33 (preprint astro-ph/0010210).>

Ćirković, M. M. and Bostrom, N. 2000, Astrophysics and Space Science 274, 675.

Ćirković, M. M. and Radujkov, M. 2001, Serbian Astronomical Journal 163, 53 (preprint astro-ph/ 0112543).

Davies, P. C. W. 1994, The Last Three Minutes (Basic Books, New York).

Dugić, M., Raković, D. and Ćirković, M. M. 2000, contributed paper to 3rd International Conference on Cognitive Science, Ljubljana, Slovenia, October 17-19, 2000 (preprint quant-ph/0010042).

Dyson, F. J. 1960, Science 131, 1667.

Dyson, F. J. 1979, Reviews of Modern Physics 51, 447.

Frautschi, S. 1982, Science 217, 593.

Gibbons, G. W. and Hawking, S. W. 1977, Physical Review D 15, 2738.

Gott, J. R. 1993, Nature 363, 315.

Hanson, R. 1998, Burning the Cosmic Commons: Evolutionary Strategies for Interstellar Colonization, preprint available at http://hanson.gmu.edu/filluniv.pdf